Montreal: The Column Generation Capital
Between early morning squirrels and late night raccoons, the Cirque du Soleil city is definitely one of the most exciting “Research/Sport” training spots worldwide, especially in the fields of artificial intelligence (AI) and operations research (OR), which have been thriving over the last decades. Being personally excited about these two topics, and in particular the latter that has many sub-fields, I would go for calling this beautiful city: the Column Generation (CG) capital.

In this article, I will go through this extremely powerful algorithm that proved over the previous years its efficiency in tackling large-scale optimization problems. I especially seek to highlight the benefits of using this technique from a practical perspective.
History
In parallel to the computational progress, humans have been continuously modeling complex real-life problems mathematically in order to solve them more rapidly and more efficiently. With the same intention, many algorithms took place to facilitate the task, especially when the problem contains a large set of variables compared to the set of constraints. One of the main algorithms known is CG proposed implicitly by Ford and Fulkerson in their 1958 paper. In fact, they did not mention it as it is known today, i.e. CG, but they were the first to present the ideas behind it by highlighting the difficulty to deal with problems involving a large number of variables explicitly. Since then, the method has been used intensively for mixed-integer linear programming (MILP). The technique is quite successful in the linear programming (LP) context as well. The main advantage of CG is that not all possibilities need to be enumerated.

Mathematical Lexicon
The CG method involves the usage of a specific lexicon. In such a process, a subset of variables are considered and others are added later based on their benefits, i.e. cost reduction or profit maximization. The term column corresponds to constrained variables that are added during the pricing phase of the simplex method used to solve the problem. The term pricing corresponds to measuring the benefits brought by each column if it is added to the model. The main problem is decomposed into two problems. First, the master problem, also called the restricted master problem (RMP) because it contains fewer variables compared to the main one. Second, the subproblem(s) help in identifying the interesting columns among others. From a dual perspective, CG done on the primal problem is equivalent to a raw generation (RG) done on the dual problem. Similar to the simplex method, for a minimization problem, it means that if a column with a negative reduced cost is found, it is added to the RMP and this process is repeated until no more columns can be added to the RMP making CG an exact method.

Problem Reformulation
As said in the previous section, the main problem is reformulated into the RMP as well as one or more subproblem(s). To highlight this easily, we will take a famous example in the literature called the cutting stock problem (CSP) where we seek the minimization of the wasted, paper for instance, from fixed-size cutting rolls while satisfying the demand. The figure below highlights the different ways a roll of length 10 can be cut into rolls of lengths 5, 3, and 2.

The main formulation widely known of this problem is as follows:

For the CG formulation, we consider the different combinations, also called patterns, which the rolls can be cut into. For instance, a roll of size 100 can be cut into 2 rolls of 30 and 1 roll of 40. Two models are then formulated. First, the RMP, which is a minimization problem initialized using artificial variables. Second, the subproblem that will provide “good” columns based on the reduced cost. The reformulation with variables is presented below.

Algorithm Approach
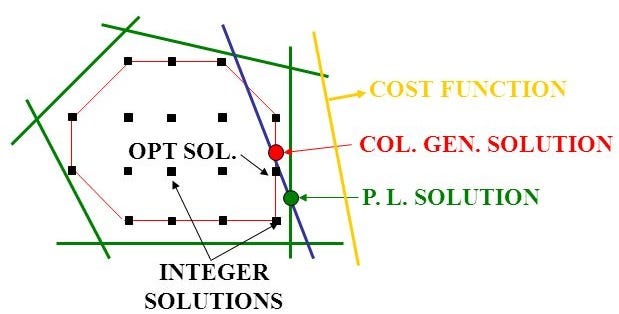
The resolution approach is iterative. First, we solve the RMP and generate the dual values that are incorporated into the subproblem in order to find the column(s) with the lowest reduced cost, for a minimization problem. The column(s) are selected and added to the RMP, which is solved again. The process keeps going until no improving columns are found. We can either stop after finding a “good” solution or go through the whole process until optimality. This algorithm is then exact. While we consider negative reduced costs for minimization problems, we look for positive reduced costs for maximization problems. From a geometrical perspective, the RMP shrinks the optimization space, which has the form of a polyhedron, to one of the faces of this polyhedron. The subproblem(s) seek the identification of an orthogonal improving direction to the vector subspace, which intersection with the polyhedron provides the face considered.

Method Benefits
As said earlier, CG is very efficient when the space of variables is large compared to the number of constraints. In such a case, we do not have to enumerate all combinations given the time complexity. Hence, CG allows a faster resolution by working on subsets of variables and through column addition if it is promising. If it is possible to reformulate a problem into a CG framework, it is a great deal. However, when it is not the case, the method cannot be applied. Hence, once the RMP and subproblem(s) are identified and designed, solving complex MILP becomes exciting. Furthermore, given that the method is iterative, solving the RMP and the subproblem(s) rapidly is a crucial aspect to consider. Otherwise, it will take a lot of time to reach good solutions. That is why we seek subproblem(s) that can be modeled as common linear problems that are solved rapidly such as the assignment problem, the knapsack problem, and others. With all these restrictions satisfied, the approach is amazing to watch and can tackle quite complex problems. Here, it is necessary to mention that, even if many use them interchangeably, CG is different than Dantzig-Wolfe decomposition. The first is the solution process used in the latter. While CG can be used independently, the decomposition helps us in building the RMP and the subproblem(s) starting from the main problem.
Real Applications
Column generation is widely used in practice such as the vehicle routing problem (VRP), aircrew scheduling (ACS), facility location problem (FLP), as well as many famous problems in the OR literature that will be presented in an upcoming article. In several businesses, CG has allowed faster resolution of complex problems while providing “good” solutions, near-optimal, or even optimal solutions based on the customer's level of satisfaction. Problems that take hours to be solved are tackled in a few minutes, sometimes a few seconds, using CG.

While still learning, I can feel the greatness of CG that confirms the quote below. When combined with Dantzig-Wolfe decomposition, this technique pushed the literature further and is leading humans to smartly tackle large-scale problems where the number of variables is extremely large.
“Simplicity is the ultimate sophistication.” — Leonardo da Vinci
As witnessed in this article, in research, simple ideas are usually the key or the starting point to tackling the most complex problems. This is a life principle that should always be highlighted in research contexts as well as others!
What do you think about this method? Can it be transferred to other areas? I am looking forward to hearing your ideas :-).
